Generación de columnas : baobab soluciones

El método de generación de columnas se utiliza para resolver de forma eficiente problemas combinatorios complejos tan diversos como el corte de barras de metal, el diseño de turnos de personal, el ruteo de vehículos, la programación de la producción o la planificación de visitas a centros por comerciales o equipos de mantenimiento. En este artículo, utilizaremos un ejemplo sencillo para explicar cómo funciona este método.

En 1954 Dantzig y Fulkerson impresionaron a la comunidad científica cuando resolvieron el problema consistente en visitar las capitales de los 49 estados de EEUU recorriendo la menor distancia posible. Más tarde, el mismo Dantzig sentó las bases de la Programación Lineal para resolver ese problema (de ese y de mayor tamaño) así como muchos otros.

Estos algoritmos (principalmente, algoritmo del Simplex y algoritmos basados en Branch-and-bound) permiten el tratamiento formal de muchos problemas y resolverlos, con la certeza de que la solución es óptima.

Sin embargo, a pesar del avance de las matemáticas y de la computación, tienen límites y a partir de cierto tamaño, por elegantes que sean, no son capaces de darnos la solución óptima a tiempo (a veces no son capaces de darnos ni siquiera una solución). Y si no tenemos una solución que llevar a la práctica, el algoritmo es estéril. Por ejemplo, en un problema de ruteo, si no obtenemos ni siquiera una ruta de reparto, por mediocre que pueda ser, de nada sirve el algoritmo.

Para atender a esto, la comunidad científica ha desarrollado multitud de estrategias para sobreponerse a esa limitación. Desde algoritmos bioinspirados (en las hormigas o en las abejas) hasta métodos analíticos sofisticados e ingeniosos que permiten «hacer trocitos» el problema de forma inteligente y sin perder rigor. Aquí nos ocupamos de una de estas segundas técnicas: las llamadas descomposiciones y en particular de una «descomposición basada en generación de columnas».

La primera aplicación de este método sobre un caso real fue publicada por Gilmore y Gomory en 1961 que lo utilizaron para decidir cómo cortar de forma eficiente barras metálicas, bobinas de papel o rollos de tela a partir de rollos con longitudes superiores. Sin embargo, su uso se extiende en la actualidad a problemas tan diversos como el diseño de turnos de personal, el ruteo de vehículos, la programación de la producción o la planificación de visitas a centros por comerciales o equipos de mantenimiento.

En este artículo, utilizaremos un ejemplo sencillo del problema del corte unidimensional para explicar cómo funciona este método.

En el ejemplo elegido tenemos barras de 200 cm, una demanda de productos con longitudes inferiores (600 unidades de barras de 40 cm, 500 unidades de barras de 60 cm y 400 unidades de barras de 70 cm) y queremos determinar cuál es el número mínimo de barras necesarias y cómo se deben cortar para satisfacer la demanda.

La solución a este problema no es evidente, ya que existen múltiples patrones de corte. Por ejemplo, las barras de 200 cm podrían cortarse en cinco productos de 40 cm sin generar material sobrante, en tres productos de 60 cm con un sobrante de 20 cm, etc.

Una forma de resolver este problema sería determinar todos los patrones de corte posibles para las barras iniciales y utilizar un modelo de programación lineal que determine cuál es el número mínimo de barras necesarias y cómo deben ser cortadas para satisfacer la demanda de productos finales. Sin embargo, ¿qué pasaría si tuviéramos barras iniciales con diferentes longitudes y/o más de tres tipos de productos finales? En este caso, el cálculo de todos los patrones de corte posibles podría convertirse en un problema en sí mismo y el tiempo de resolución del modelo de optimización aumentaría de forma exponencial a medida que aumentase el número de patrones a tener en cuenta.

Una alternativa para abordar este problema de forma eficiente es aplicar el método de generación de columnas. Este método se utiliza para resolver problemas de programación lineal donde todas las variables del problema (o columnas) no son conocidas de antemano o donde es poco práctico generarlas desde el inicio.

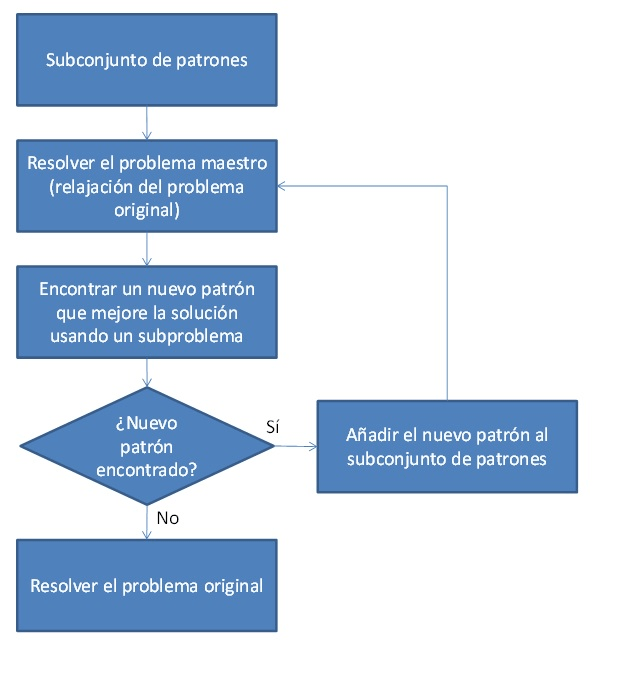
El método parte de un problema maestro que es una relajación lineal del modelo de programación lineal original (problema donde todas las variables son reales y por tanto, no existen variables enteras ni binarias). Este problema se resuelve para un conjunto reducido de variables, columnas o, en nuestro ejemplo, patrones de corte con el objetivo de determinar el número mínimo de barras iniciales y cómo deben ser cortadas para satisfacer la demanda y una vez resuelto, se busca si existe alguna nueva variable, columna o patrón que mejore la solución inicial (en nuestro caso, que consiga reducir el número de barras iniciales necesarias para satisfacer la demanda) haciendo uso de un subproblema. Este proceso iterativo se repite hasta que no se encuentre ningún nuevo patrón que mejore la solución del problema maestro, momento en el cual se resuelve el problema original (problema maestro sin relajar donde sí pueden existir variables enteras y/o binarias además de variables reales) con los patrones iniciales y con los patrones generados hasta el momento.

Pasos del método de generación de columnas

1. Subconjunto inicial de patrones

Para inicializar el método, vamos a utilizar un conjunto de patrones sencillo de generar. En particular, utilizaremos tres patrones y en cada uno de ellos sólo permitiremos cortes de un tipo de producto final. De esta forma, el patrón 1 indica que la barra inicial será cortada en cinco productos de 40 cm, el patrón 2 representa que la barra inicial será cortada en tres productos de 60 cm y el patrón 3 muestra que la barra inicial será cortada en dos productos de 70 cm.

Subconjunto inicial patrones generación columnas

2. Problema maestro

El problema maestro (relajación lineal del modelo de programación original donde todas las variables son reales) que vamos a utilizar presenta la siguiente formulación:

La variable de decisión 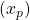$(x_p)$ representa el número de barras iniciales de longitud 200 cm que serán cortadas mediante el patrón de corte 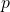$p$ y es de tipo real.
Existe una restricción que controla que la suma de los productos finales 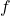$f$ (40 cm, 60 cm y 70 cm) cortados a partir de cada patrón 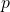$p$ satisfaga la demanda.
Tenemos una función objetivo para minimizar el número de barras iniciales a utilizar.

Formulación del problema maestro

Índices:

$p$ $patrones$ $de$ $corte$

$f$ $productos$ $finales$

Parámetros:

$d_f$ $demanda$ $del$ $producto$ $final$ $f$

$a_f_p$ $número$ $de$ $productos$ $finales$ $f$ $en$ $el$ $patrón$ $de$ $corte$ $p$

Variable:

$x_p$ $número$ $de$ $barras$ $iniciales$ $cortadas$ $usando$ $el$ $patrón$ $de$ $corte$ $p$

Minimizar:

$\begin{align*} \sum_{p}x_{p} \end{align*}$

Sujeto a:

$\begin{align*} \sum_{p} a_{fp}x_{p} \geq d_{f} \hspace{1cm} \forall f\\ x_{p} \geq 0, real \hspace{1cm} \forall p \end{align*}$

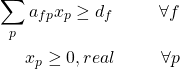
3. Subproblema

La formulación del subproblema es la siguiente:

La variable de decisión 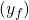$(y_f)$ corresponde con el número de productos finales de longitud 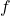$f$ (40 cm, 60 cm o 70 cm) incluidos en el nuevo patrón y es de tipo entero.
Existe una restricción que controla que la suma de las longitudes de los productos incluidos en el nuevo patrón no supere la longitud de la barra inicial.
Tenemos una función objetivo que que maximiza el valor de los productos introducidos en el nuevo patrón a través de los precios sombra del problema maestro 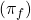$(\pi_f)$ . En este caso, para que un patrón sea finalmente elegido y pase a formar parte del conjunto de patrones con los que trabajará el problema maestro en la siguiente iteración, deberá alcanzarse un valor de la función objetivo superior a 1 para ese patrón. Si esto es así, el coste reducido del nuevo patrón en el problema maestro será negativo lo que quiere decir que la función objetivo de este problema se verá reducida en 1 menos el valor de la función objetivo del subproblema por cada barra que se corte en el problema maestro usando el nuevo patrón, lo que se traduce en un ahorro en el número de barras finalmente empleadas para cubrir la demanda.

Formulación del subproblema

Índices:

$f$ $productos$ $finales$

Parámetros:

$\pi_f$ $precio$ $sombra$ $asociado$ $con$ $la$ $restricción$ $de$ $demanda$ $f$ $en$ $el$ $problema$ $maestro$

$w_f$ $longitud$ $del$ $producto$ $final$ $f$

$W$ $longitud$ $de$ $la$ $barra$ $inicial$

Variable:

$y_f$ $número$ $de$ $productos$ $finales$ $f$ $incluidos$ $en$ $el$ $patrón$ $de$ $corte$

Maximizar:

$\begin{align*} \sum_{f}\pi_{f}y_{f} \end{align*}$

Sujeto a:

$\begin{align*} \sum_{f} w_{f}y_{f} \leq W \hspace{1cm} \forall f\\ y_{f} \geq 0, entero \hspace{1cm} \forall f \end{align*}$

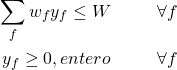
Inicializando el método con los tres patrones de partida, el subproblema ha generado los dos nuevos patrones que aparecen en la siguiente tabla, donde, por ejemplo, el patrón 4 propone cortar la barra inicial en un producto de 60 cm y en dos de 70 cm.

4. Generación de columnas

Antes de generar patrones haciendo uso de la descomposición se disponía de tres patrones y el número mínimo de barras necesarias para atender la demanda haciendo uso de esos patrones es 487.

Haciendo uso de los patrones generados con la descomposición de los originales, cinco en total, se ha obtenido que se debería comprar un total de 410 barras y que 60 de ellas deberían ser cortadas siguiendo el patrón 1 (cinco productos de 40cm), 200 siguiendo el patrón 4 (un producto de 60cm y dos productos de 70cm) y 150 siguiendo el patrón 5 (dos productos de 40cm y dos productos de 60cm).

Esta solución cumple exactamente con la demanda de productos finales y es óptima al emplear el menor número de barras iniciales posible, además de no generar ningún desperdicio durante el proceso de corte.

Para problemas de carácter combinatorio como el planteado anteriormente, el método de generación de columnas permite explorar el espacio de soluciones de forma rápida e inteligente a partir de un conjunto reducido de variables o columnas de partida, lo que hace que el tiempo de ejecución de este método crezca de forma razonable cuando aumenta el tamaño del problema.

En este ejemplo, la descomposición solo ha generado dos patrones nuevos y el problema completo ha considerado solo cinco. En un problema pequeño se podrían generar todos los posibles patrones sin necesidad de la generación de columnas y que el problema trabajara con todos ellos. Sin embargo, en la medida en la que hubiese más productos finales (con diferentes longitudes) el número de posibles patrones podría ser extremadamente elevado y el problema, con todos esos patrones, no se podría resolver en tiempos razonables. En este caso, interesa generar solo un conjunto inicial y, después, mediante la descomposición ir añadiendo solo nuevos patrones potencialmente interesantes.

Este método es una estrategia sofisticada de divide y vencerás, no incluida en solvers comerciales como Gurobi, pero especialmente útil no sólo para resolver problemas del corte sino problemas complejos relativos al diseño de turnos de personal, al ruteo de vehículos, a la programación de la producción o a la planificación de visitas a centros por comerciales o equipos de mantenimiento.

1. Subconjunto inicial de patrones

2. Problema maestro

Formulación del problema maestro

Índices:

Parámetros:

Variable:

Minimizar:

Sujeto a:

3. Subproblema

Formulación del subproblema

Índices:

Parámetros:

Variable:

Maximizar:

Sujeto a:

4. Generación de columnas

También podría gustarte

La solución al acertijo de Einstein

Aprendizaje Federado (FL): Protege tus datos y potencia tu estrategia con IA.

6 claves para implantar proyectos de analítica avanzada en tu empresa.