El problema del viajante
El problema del viajante (por sus siglas en inglés TSP) consiste en encontrar el camino único más corto que, dada una lista de ciudades y las distancias entre ellas, visita todas las ciudades una sola vez y regresa a la ciudad de origen.
Su origen no está claro. Un manual alemán para viajantes de 1832 menciona el problema e incluye viajes de ejemplo por Alemania y Suiza, pero no cubre sus matemáticas.
La primera formulación matemática fue realizada en el siglo XIX por W.R. Hamilton y Thomas Kirkman. El juego icosiano de Hamilton era un rompecabezas recreativo basado en encontrar un ciclo hamiltoniano, que en realidad es una solución al problema de TSP en un grafo (nota: el TSP es el ciclo hamiltoniano de menor longitud en un grafo conexo).
El TSP se puede formular como un modelo de Programación Lineal Entera. Aunque se conocen varias formulaciones para resolver este problema, dos de ellas son las más destacadas: la propuesta por Miller, Tucker y Zemlin, y la propuesta por Dantzig, Fulkerson y Johnson.
En teoría, estos métodos pueden devolver una solución óptima al problema, pero como éste se considera un problema NP-difícil, pueden ser demasiado costosos tanto en potencia de cálculo como en tiempo.
Con el fin de obtener buenas soluciones en un tiempo más corto, se ha realizado un gran esfuerzo para intentar resolver este problema con una variedad de métodos heurísticos. De todo este grupo de heurísticas, nos gustaría destacar las inspiradas en la biología: Optimización por Colonia de Hormigas y Algoritmos Genéticos (GA).
Programación Lineal Entera
Como mencionamos, existen dos formulaciones principales para el TSP, el propuesto Miller, Tucker y Zemlin (MTZ) y el Dantzig, Fulkerson y Johnson (DFJ). Aunque la formulación DFJ es más fuerte, la formulación MTZ puede ser útil.
Formulación MTZ
La formulación matemática propuesta por Miller, Tucker y Zemlin es la siguiente:

Usando este conjunto, las dos variables y el parámetro, podemos formular el problema como:
![Rendered by QuickLaTeX.com \[min \sum_{i=1}^{n}\sum_{j\neq i,j=1}^{n}c_{ij}x_{ij}\]](https://baobabsoluciones.es/wp-content/ql-cache/quicklatex.com-889a4bf6b9925d0d79a80181d5acf5cf_l3.png)
Sujeto a:
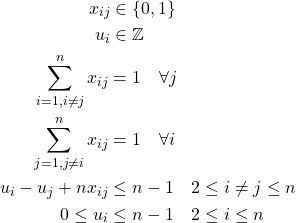
La primera y la segunda ecuaciones refuerzan el tipo de las diferentes variables, la tercera y la cuarta ecuaciones aseguran que cada nodo sea alcanzado y abandonado solo una vez, mientras que las dos últimas ecuaciones imponen que solo una ruta cruce todos los nodos.
Formulación DFJ
En la formulación propuesta por Dantzig, Fulkerson y Johnson partimos de la misma variable x_ {ij} y parámetro c_ {ij}> 0 para que la formulación se pueda completar con:
![Rendered by QuickLaTeX.com \[min \sum_{i=1}^{n} \sum_{j \neq i, j=1}^{n} c_{ij}x_{ij}\]](https://baobabsoluciones.es/wp-content/ql-cache/quicklatex.com-6fbb1a77a284dd77896d330585863d26_l3.png)
Sujeto a:
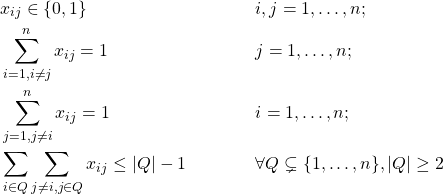
Las tres primeras ecuaciones son las mismas que en la formulación anterior, y la nueva restricción (la última) asegura que no haya sub-recorridos, por lo que la solución devuelta es un recorrido único y no la combinación de recorridos más pequeños. Debido a que esto conduce a un número exponencial de posibles restricciones, en la práctica se resuelve con una generación de columnas retrasada.
En el siguiente gráfico podemos ver la solución óptima para un problema de 100 nodos.
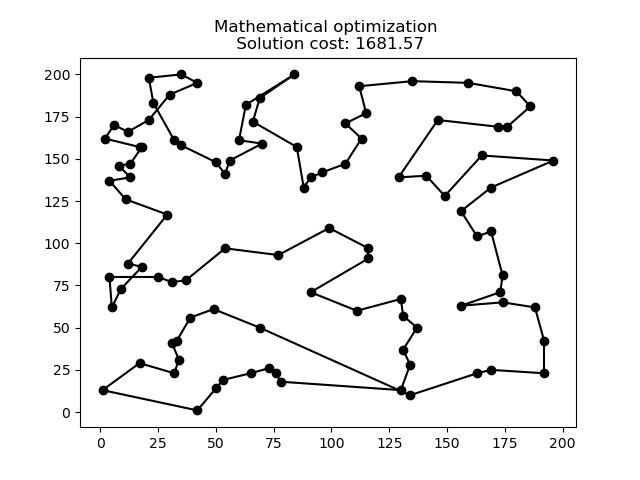
Optimización por Colonia de Hormigas
También conocido como Ant Colony System (ACS) o Ant System (AS), es una técnica probabilística o heurística utilizada para resolver problemas que se pueden reducir a encontrar buenos caminos sobre grafos. Este método fue propuesto inicialmente por Marco Dorigo en 1992 en su tesis doctoral.
En la siguiente animación se puede ver cómo esta heurística funciona para un problema y evoluciona mejorando la solución con el tiempo.
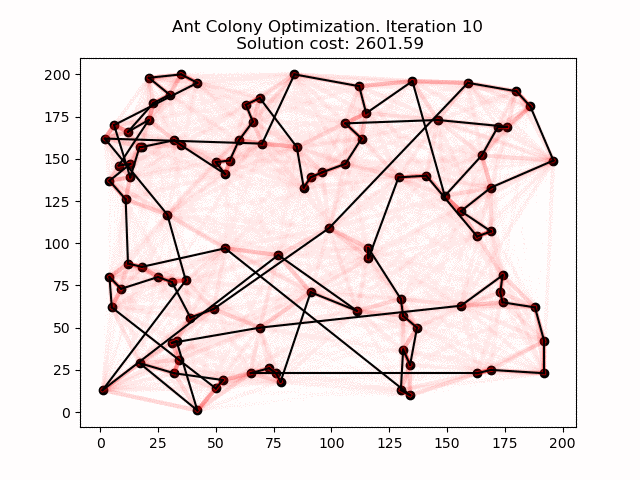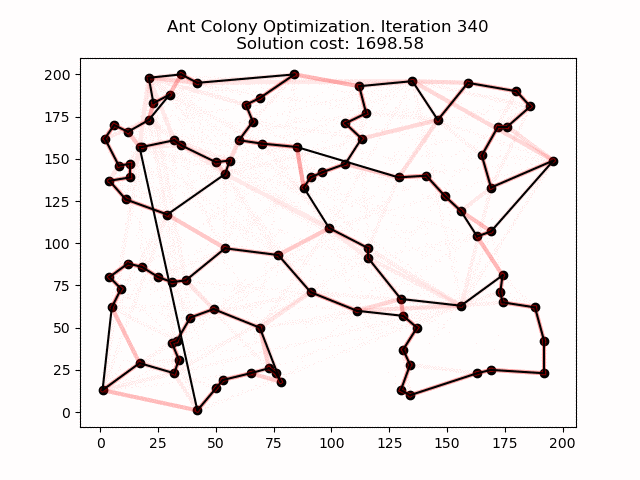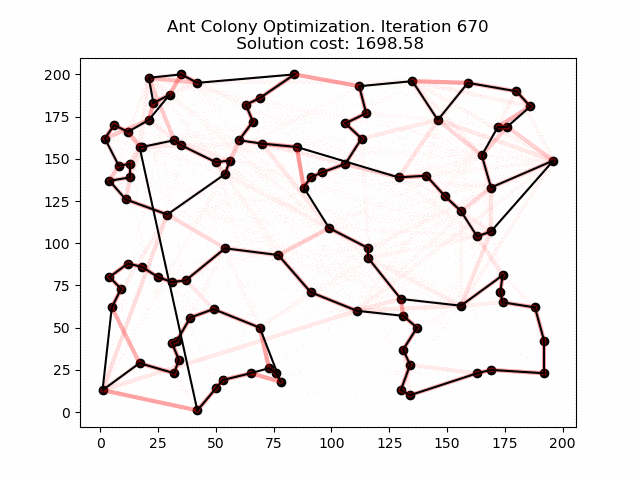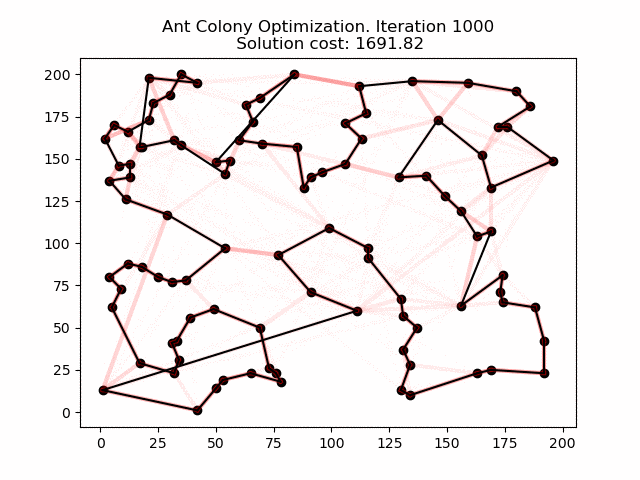
En la animación, las sombras rojas representan la cantidad de feromonas depositadas por las hormigas durante los cálculos.
¿Quieres estar al día con blogs como este? Suscríbete a nuestro Newsletter bimensual.
Algoritmos Genéticos
Los Algoritmos Genéticos (GA) son heurísticos inspirados en el proceso de evolución de los seres vivos. Cada solución es un cromosoma compuesto por genes que representan los diferentes valores de las variables de la solución.
Comenzando con una población inicial, podemos hacer que las soluciones “evolucionen” en iteraciones. El proceso consiste en seleccionar la mejor mitad de la población de la que elegimos al azar pares de cromosomas (soluciones) para el apareamiento. En estos apareamientos intercambiamos genes de ambas soluciones para generar nuevas soluciones (hijos).
Después del proceso de apareamiento, aplicamos mutaciones al azar en los hijos resultantes para explorar más a fondo el espacio de la solución.
Finalmente seleccionamos los mejores 50 individuos de la población (el inicial más los hijos) y continuamos el proceso hasta que convergemos en una solución.
En la siguiente animación podemos ver cómo evoluciona el Algoritmo Genético para el mismo problema de 100 puntos.
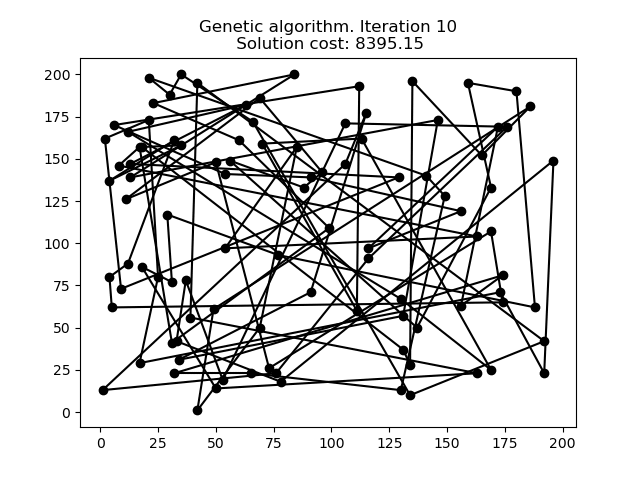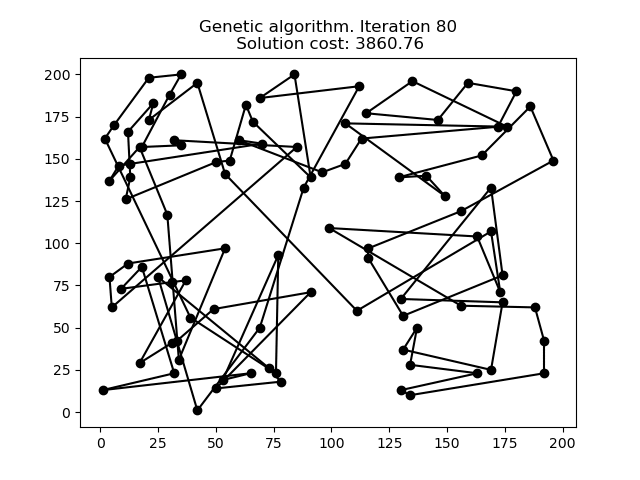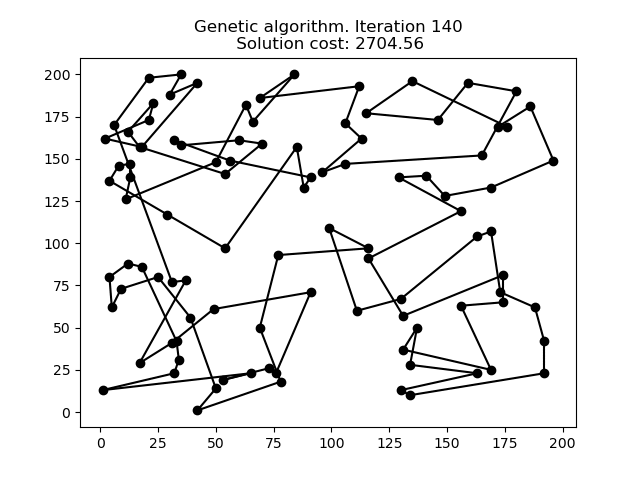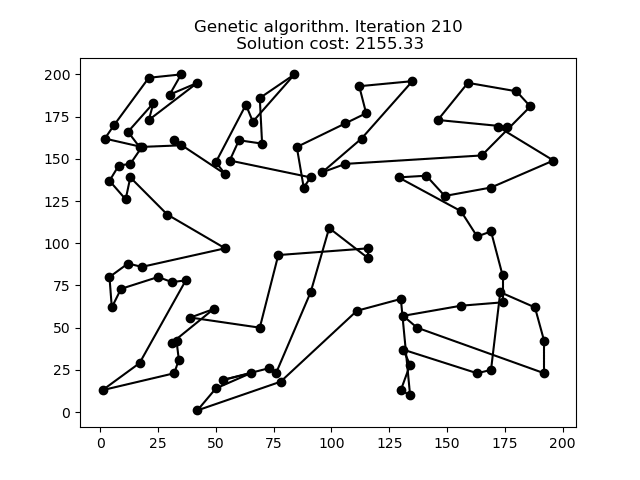
Comparación
Como se puede ver en los gráficos anteriores, cada heurístico proporciona una solución al problema, aunque algunas mejores que otras. Cuando probamos estos tres métodos en más conjuntos de datos, podemos encontrar los siguientes resultados:
| LP | LP | ACO | ACO | GA | GA | |
|---|---|---|---|---|---|---|
| Nodes | Perf. | Time | Perf. | Time | Perf. | Time |
| 5 | – | 0.06s | – | 0.04s | – | 0.08s |
| 10 | – | 0.17s | 3.22% | 0.2s | – | 0.1s |
| 25 | – | 0.72s | 23.68% | 1.09s | 28.94% | 0.17s |
| 50 | – | 1.75s | 26.42% | 4.04s | 66.04% | 0.24s |
| 75 | – | 3.04s | 14.67% | 11.61s | 84.00% | 0.33s |
| 100 | – | 6.43s | 11% | 16.32s | 96.00% | 0.44s |
| 150 | – | 16.73s | 6.67% | 180.69s | 70.00% | 2.78s |
| 200 | – | 56.17s | 5.00% | 267.42s | 92.50% | 3.47s |
| 250 | – | 252.06s | 3.60% | 503.31s | 90.80% | 7.58s |
El rendimiento se calcula como la desviación entre la solución proporcionada por cada método y la mejor solución encontrada para esa instancia.
En instancias muy pequeñas, todos los métodos alcanzan la solución óptima, pero a medida que las instancias se hacen más grandes, los heurísticos comienzan a desviarse de la mejor solución encontrada por el programa lineal de enteros. Aunque el Algoritmo Genético muestra una mayor desviación de la solución óptima, aún puede proporcionar una solución en un tiempo más corto que los otros métodos. Probablemente, si tuviéramos que aumentar la población para explorar mejor el espacio de la solución, podríamos obtener mejores resultados sin sacrificar el tiempo de procesamiento.
ACO es la heurística (y la diseñada exclusivamente para este problema) que puede seguir el modelo exacto, pero tarda más en llegar a una solución.
Para resolver el modelo lineal de enteros necesitamos un solver matemático, que puede ser gratuito o comercial. Para esta publicación utilizamos un solver comercial que en realidad mejora el rendimiento exponencialmente en comparación con los gratuitos. Esta ventaja es lo que hace que el problema lineal de enteros sea más rápido que ACO. Si tuviéramos que probar el software libre, ACO proporcionaría mejores soluciones en menos tiempo, utilizando un lenguaje de código abierto (Python).
Si te gusta resolver problemas como este, baobab es tu sitio. Consulta nuestras ofertas de trabajo.
Puedes ver aquí cómo se desarrollan estos algoritmos para resolver el problema del viajante con Python.
Autor: Guillermo González-Santander, Jefe de Proyectos en baobab.