Blog

Uno de los retos más importantes a los que se enfrentan los departamentos de trading de energía es el tratamiento de la incertidumbre para tomar decisiones de compra y venta. En este artículo explicaremos, con un ejemplo muy sencillo, en qué consiste la optimización de estas decisiones en mercados con incertidumbre, donde las predicciones con las que se trabaja no son suficientemente fiables debido a la volatilidad del entorno.

Para este ejemplo usaremos primero técnicas deterministas, y a continuación, técnicas estocásticas en las que se trata la incertidumbre. Estas técnicas son aplicables a decisiones de trading de electricidad, gas, hidrocarburos u otras materias primas.

Ejemplo de optimización lineal determinista

A efectos de simplificar este ejemplo, suponemos que el trader tiene que tomar decisiones de venta de materia prima en toneladas, pero podría haberse tratado de compra de energía eléctrica en MWh. Además, simplificando más:

• Nos vamos a centrar en los excedentes de una única materia prima para un mes concreto.
• Tenemos una cantidad fija que vender ese mes.
• Operamos en dos mercados donde podemos vender ese excedente.
• Cada mercado tiene un precio de venta y unas condiciones de mercado diferentes.

El objetivo es determinar la decisión óptima con un conjunto dado de restricciones:

• 20.000 t de una materia prima a vender en un mes.
• En el mercado 1 tenemos un contrato cerrado con una cantidad mínima que satisfacer de 6.000 t y el precio de venta es 1 u.m./t.
• En el mercado 2 se puede comprar como máximo 15.000 t y el precio de venta es 1,5 u.m./t.

Para encontrar la solución óptima, lo primero es formular el problema:

• Variables de decisión – X_i: t a vender en cada mercado, donde i es 1 o 2  (mercado 1 o mercado 2)
• Función objetivo – Max Z=1·X₁ +1,5·X₂
• Restricciones:
  • X₁ ≥ 6.000
  • X₂ ≤ 15.000
  • X₁ + X₂ ≤ 20.000
  • X₁,X₂ ≥0

Y en este caso, con solo dos mercados, podríamos encontrar la solución óptima representando las restricciones y la función objetivo en una gráfica con dos ejes, uno para cada mercado:

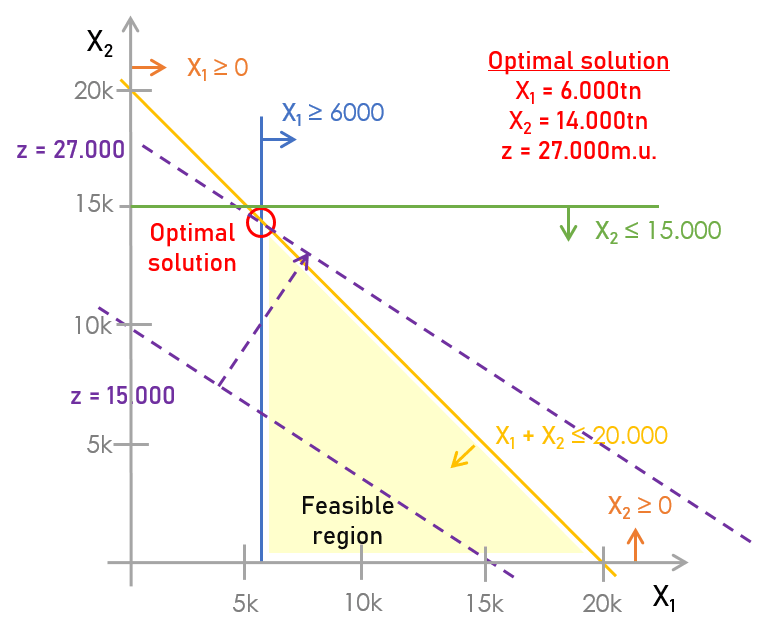
La decisión óptima es, entre todas las posibles, vender 6.000 t en el mercado 1, 14.000 t en el mercado 2, obteniendo por esta venta un total de 27.000 unidades monetarias (€, $ o la moneda que se use).

En un escenario real, el problema puede ser mucho más complejo con más materias primas cuyos excedentes se quieren vender, incrementando el número de meses que se evalúan de forma simultánea, bajando la decisión a nivel diario o ampliando las restricciones de venta en cada mercado.

Y, en relación a este último aspecto, el problema se puede complicar cuando, por ejemplo, existe una cantidad mínima por contrato para un conjunto de meses y una cantidad mínima por mes, cantidades mensuales múltiplo de una cantidad que corresponde con la capacidad del medio de transporte o mercados en los que se vende a un precio diferente según la calidad de la materia prima  o según los volúmenes de venta.

En definitiva, encontrar la solución óptima en entornos de trading reales no es algo trivial, y se requiere usar técnicas de Analítica Prescriptiva para asegurarnos de que la decisión no solo es buena, sino que es la óptima matemática. Los traders que toman decisiones óptimas obtienen mayores márgenes que los que toman decisiones que solo son buenas.

Optimización lineal bajo incertidumbre

Pero el problema real de optimización todavía es más complejo. ¿Qué pasa si tenemos en cuenta la incertidumbre?

Veámoslo:

Si no tratamos la incertidumbre, todos los parámetros (c_i=coeficientes que multiplican a las variables decisión en la función objetivo, a_ij=coeficientes que multiplican a las variables decisión en las restricciones y b_j=coeficientes que aparecen en el extremo derecho de las restricciones) se conocen con certeza.

Sin embargo, si tenemos en cuenta la incertidumbre, uno o varios parámetros del modelo no se conocen con certeza, pero sí se conoce su distribución de probabilidad o un conjunto de escenarios posibles (valor del parámetro más probabilidad asociada).

Existen distintos enfoques para tratar la incertidumbre:

• Optimización estocástica. Dado un conjunto de escenarios (valores de los parámetros de incertidumbre y probabilidades asociadas), se quiere obtener una solución factible que maximice el beneficio esperado o que minimice los costes esperados para el conjunto completo.

• Chance constraints optimization. Este caso es una variante del anterior, donde alguna de las restricciones del modelo se satisfacen con una determinada probabilidad. Por ejemplo, si una restricción de azar tiene una probabilidad del 95%, esto significa que la restricción debe satisfacerse para (al menos) el 95% de los escenarios analizados. Este enfoque se puede utilizar cuando se quiere dar menos peso a los escenarios que ocurran menos veces.

• Optimización robusta. Dado un conjunto de incertidumbre en el que se pueden mover los parámetros de incertidumbre (conjunto en formato caja o elipse, por ejemplo), se busca diseñar soluciones factibles y próximas al óptimo. En este caso es más importante la factibilidad que la optimalidad.

Optimización estocástica

Vamos a estudiar una variante algo más compleja del problema anterior usando optimización estocástica.  

En particular, vamos a suponer diferentes escenarios de precios de los productos. Este es el caso más elemental y permite ilustrar la esencia de la optimización estocástica. Sin embargo, existen variantes más complejas y mucho más potentes. Por ejemplo, puede haber diferentes escenarios de demanda o, incluso, se pueden considerar las compras para diferentes períodos y los diferentes escenarios de precio y demanda en cada uno de ellos (modelos multi-etapa).

• Misma cantidad de excedente.
• Tres mercados:
  • Mercado 1. Ahora, podemos decidir si vender o no en este mercado, pero si vendemos, tenemos que vender como mínimo 6.000 t.
  • Mercado 2. Mismas condiciones que antes, solo se pueden vender como máximo 15.000 t.
  • Mercado 3. Nuevo mercado sin límites mínimos ni máximos de venta.
• Tres escenarios de precios cada uno con una probabilidad asociada (0,4, 0,2 y 0,4 respectivamente). En este caso, la estocasticidad está en c_i (precio de venta).

Este problema ya no se puede resolver de forma gráfica porque ya no tenemos solo dos variables.

Modelo determinista vs. Modelo estocástico

Modelo determinista. Se utiliza este modelo para evaluar cada escenario de forma independiente. Como resultado, se tienen tres soluciones: mejor solución para cada uno de los escenarios deterministas planteados.

Modelo estocástico. Se utiliza este modelo para evaluar los tres escenarios de forma conjunta. Como resultado, se tiene una única solución para el conjunto de los tres escenarios.

¿Cuál es la mejor solución?

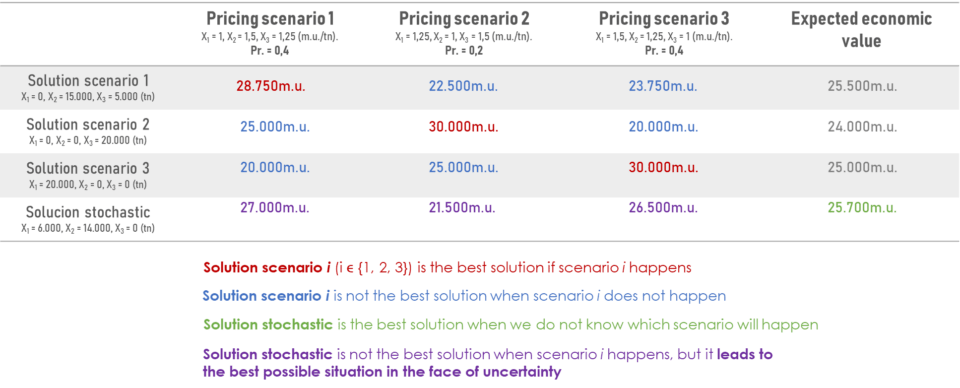
Las conclusiones de la comparativa aparecen recogidas en esta tabla, donde se evalúa cada una de las cuatro soluciones anteriores ante los tres escenarios de precios.

Analizadas todas las soluciones, se ve que la solución estocástica es la que obtiene un mejor valor económico esperado.

Conclusiones

Los traders toman todos los días decisiones de compra y venta de una gran complejidad. En la medida de que dispongan de mejores herramientas, van a ser capaces de tomar mejores decisiones, y a la larga, obtener mayores márgenes en sus operaciones.

La mente humana es capaz de encontrar soluciones buenas a problemas como los que hemos tratado de decisiones de trading, pero difícilmente puede encontrar la óptima. Y menos aun si además tenemos en cuenta la incertidumbre, por muy buenas que sean las predicciones que tengan a su disposición los traders. Y es aquí donde las herramientas de Analítica Prescriptiva marcan la diferencia para obtener márgenes mayores en las operaciones de trading.