El problema del viajante
En blogs anteriores ya hemos introducido este problema y alguna de las formas típicas para resolverlo. En esta ocasión vamos a introducir nuevos métodos de resolución y ampliar la comparación que realizamos previamente para tener en cuenta estos nuevos métodos.
1.- Método 2-opt y 3-opt
Ambos métodos son métodos simples de búsqueda local específicos del problema del TSP. El método 2-opt fue propuesto en 1958 por Croes. Este método consiste en seleccionar dos arcos del grafo completo, eliminarlos y evaluar la otra posición de reconexión del grafo que permite obtener un menor coste. En la siguiente imagen se puede ver un ejemplo de este proceso:
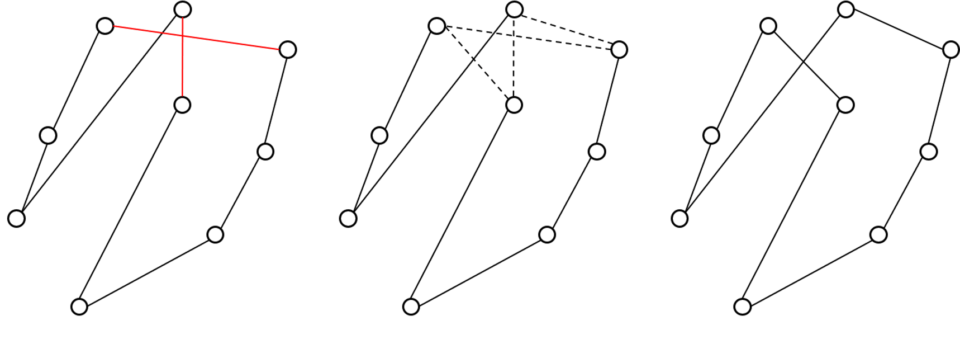
Figura 1. Ejemplo método 2-opt .
Los arcos rojos son los que se estudian, que se eliminan y se escoge cuál de las dos posibles conexiones es la mejor, la existente o la nueva que se genera en este caso.
El método 3-opt es una extensión del anterior, de tal forma que en este caso son 3 arcos los que se eliminan y se evalúan las conexiones que no generan sub-ciclos. De nuevo en la siguiente figura se puede ver un ejemplo.
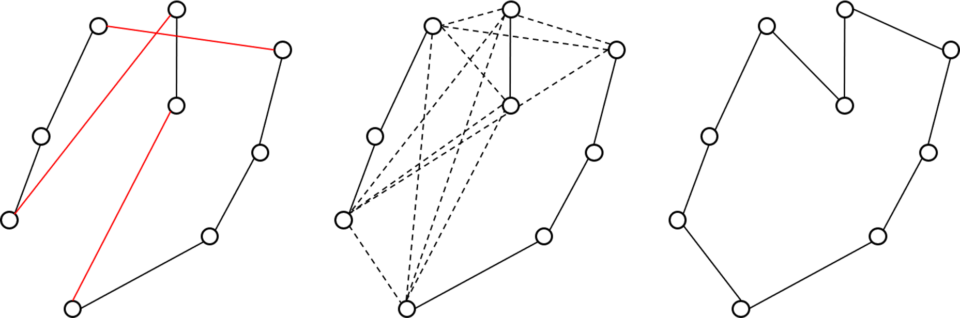
Figura 2. Ejemplo aplicación método 3-opt.
Podemos ver como aplicando un cambio 3-opt somos capaces de encontrar una mejor solución desde el mismo punto de partida que con el cambio 2-opt.
Por norma general el método 3-opt es más lento, su complejidad es O(n^3), que el método 2-opt pero a su vez suele generar soluciones mejores.
2.- Recocido simulado
En este caso el recocido simulado es una técnica metaheurística para aproximar el máximo o mínimo global de una función. En este caso utilizamos el recocido simulado combinado con las técnicas 2-opt y 3-opt.
El recocido simulado, inspirado en el proceso de recocido en la metalurgia, consiste en el establecimiento de una temperatura, la cual se va reduciendo según pasan las iteraciones del método. Esta temperatura se usa para regular la aceptación de cambios en el problema que no supongan una mejor solución, de tal forma, que a mayor temperatura, mayor probabilidad de aceptar una solución «peor».
Este proceso permite explorar de mejor forma el espacio de soluciones y por tanto lograr encontrar una mejor solución.
En nuestro caso, si al evaluar una configuración con el 2-opt o 3-opt obtenemos una solución de valor frente al inicial, en los métodos normales sólo las aceptaríamos si c0>c1 , pero en el recocido simulado se introducen cambios en este proceso:
- Primero se obtiene un número aleatorio entre 0 y 1.
- Si la temperatura es mayor que dicho número y se acepta el cambio.
- En caso contrario se continúan las iteraciones.
3.- Comparación
Para llevar a cabo la comparación de estos métodos hemos generado 10 ejemplos para problemas de 10, 25, 50, 100, 150 y 200. Los resultados que se presentan son por lo tanto los medios para cada tamaño de problema.
Además, en este caso incluimos también la formulación DFJ presentada en el anterior artículo para comparar sus resultados. En el caso de los modelos enteros se ha usado el solver SCIP dado que recientemente ha liberado su uso.
Por lo tanto, los modelos a comparar son:
- Modelo entero DFJ (DFJ).
- Algoritmo genético (GA).
- Colonia de hormigas (ACO).
- 2-opt (2OPT).
- 3-opt (3OPT).
- Recocido simulado 2-opt (SA2OPT).
- Recocido simulado 3-opt (SA3OPT).
En la primera tabla se puede ver para cada método comparado con el mejor (DFJ) su desviación, mientras que en la segunda se puede ver el tiempo medio, en segundos, necesario para alcanzar dichas soluciones por cada uno de los métodos. Merece la pena destacar que para las instancias de 200 nodos el método exacto (DFJ) no ha sido capaz de obtener una solución por lo que la comparación se hace con 9 instancias.
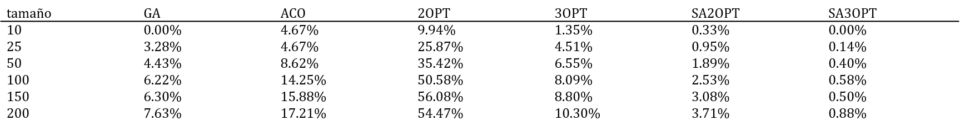
Tabla 1. Método de comparación.
Cómo se puede comprobar algunos métodos se quedan muy cerca de obtener el óptimo local hasta en tamaños de instancias grandes. Al igual que en el blog el anterior los resultados del algoritmo genético son muy buenos, mientras que, en este caso el ACO ha sufrido peores resultados al limitar el tiempo de ejecución para obtener soluciones.
Los nuevos métodos presentan distintas calidades de resultados, mientras que el 2OPT es el peor de todos, lo cual es de esperar dado su carácter determinista y su limitación a la hora de realizar cambios. El 3OPT presenta resultados mejores y cercanos a los del algoritmo genético.
Finalmente, la versión de estos dos métodos con recocido simulado mejora considerablemente y en el caso del SA3OPT se obtienen los mejores resultados de cualquier método.
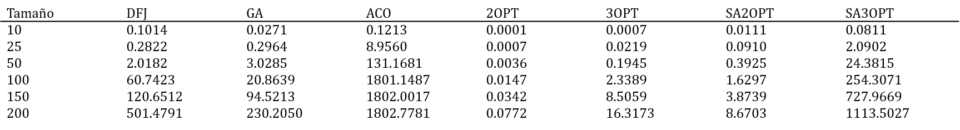
Tabla 2. Método de comparación.
Tal y como se muestra en la tabla de tiempos, muchos de los métodos heurísticos y metaheurísticos son capaces de encontrar las soluciones en menor tiempo, a excepción del ACO y el SA3OPT. En el caso del primero, se debe a la alta complejidad computacional de alguno de los cálculos necesarios del metaheurístico, mientras que, en el caso del SA3OPT, dado el alto número de combinaciones posibles y el proceso del recocido simulado hace que su tiempo de ejecución sea tan elevado.
Vistos los resultados y los tiempos medios de ejecución, cabe la posibilidad de que en ciertas circunstancias sea de alto interés utilizar alguna de las técnicas heurísticas o metaheurísticas.
Si te gusta resolver problemas como este, baobab es tu sitio, consulta nuestras ofertas de trabajo, y si sientes curiosidad por ver como se han resuelto estos problemas aquí tienes todo el código.
REFERENCIAS
- Croes, G. A. (1958). A method for solving traveling-salesman problems. Operations research, 6(6), 791-812.


