
La teoría de juegos puede proporcionar un valioso punto de vista para la toma de decisiones.
Diariamente, cada empresa se enfrenta a decisiones complejas sobre su operativa. Para algunas de estas decisiones, el resultado de la decisión no está condicionado por las decisiones de otros, pero en muchas ocasiones no es así. El resultado no sólo depende de la acción o estrategia adoptada, sino que también se ve afectado por las decisiones de otros.
Puede ser sencillo decidir mejorar las predicciones de la demanda de los clientes o automatizar el proceso productivo si el retorno de la inversión es positivo. Sin embargo, cuando la toma de decisiones abarca aquellas de carácter más estratégico e involucra a más agentes, no sólo puede resultar complejo cuantificar los resultados de dichas acciones, sino también, interpretarlos.
En este sentido, surgió una rama de las matemáticas conocida como la teoría de juegos, que está muy relacionada con la economía del comportamiento (Behavioral Economics). La teoría de juegos permite representar mediante simplificaciones (juegos) las situaciones comunes de competencia o colaboración de unos agentes, lo que permite determinar la mejor estrategia ante cada situación, dado el comportamiento previsto de los jugadores. A continuación, vamos a presentar dos ejemplos para ilustrar cómo aplicar la teoría de juegos a situaciones comunes de competencia o colaboración.
1. Juegos de competencia
Para aumentar su cuota de mercado, una empresa A puede barajar diferentes estrategias, como realizar una bajada de precios de sus productos o invertir en una campaña publicitaria. Lo primero que hará A será analizar económicamente estas opciones, por lo que tendrá estimaciones del retorno de la inversión de ambas, pero ¿es esta información suficiente?.
Si la empresa A tiene competencia, le interesará considerar también lo que va a hacer ésta. ¿Qué hará una empresa B que venda productos similares? ¿Es posible que le copie la estrategia?.
- Si ambas empresas deciden invertir en grandes campañas publicitarias incurrirán en elevados costes, pero no modificarán sus ingresos, ya que el total de clientes en el mercado sigue siendo el mismo.
- Si B no realiza dicha campaña, A se beneficiaría enormemente de hacerla y captaría los clientes de B. Y lo mismo sucedería en caso recíproco.
- Finalmente, si ninguna de las dos invirtiera, no cambiaría nada.
Dado que A analizó las alternativas de invertir y de no hacerlo, podemos representar estas decisiones en una matriz. Cada celda (a,b) contiene dos valores correspondientes, respectivamente, a los beneficios de A y B cuando A elige la estrategia de la fila (en color naranja) y B la de la columna (en color negro). Es decir, si A no invierte, pero B sí: A perdería 10 u.m. (unidades monetarias) y B ganaría 5 u.m.

Si las dos empresas escogen la misma estrategia, no aumentarán su cuota de mercado ni sus ingresos. Aunque si ambas han decidido realizar la campaña, ambas tendrán que asumir dichos costes. Mientras que, si difieren, la que haya invertido captará los clientes a la otra y con creces superará los gastos de publicidad.
Con una matriz tan sencilla se modelan los efectos de una interacción no trivial y el de los posibles resultados según las decisiones que tome cada empresa. La mejor decisión para las dos empresas, aisladamente, sería invertir. No obstante, la mejor decisión conjunta sería no hacerlo, aunque esto suponga un claro coste de oportunidad para ambas y la tentación de cambiar de estrategia en cualquier momento para ganar a la otra.
¿Se puede fiar A de que B actúe racionalmente y decida no invertir? ¿Qué ocurre si es una decisión repetida que toman todos los años, como una campaña navideña? ¿Influirá en la decisión de A lo que B decidiera hacer el año anterior? ¿Qué sucede si la matriz de resultados no es simétrica y una empresa tiene más que perder que otra? ¿O cómo cambiaría la situación si fueran más de dos empresas?.
Este juego representa una simplificación por no tener en cuenta las preguntas anteriores y muchos otros factores, sin embargo, proporciona una visión más completa de este problema y aporta información valiosa que no se habría tenido en cuenta si A hubiese considerado únicamente los ingresos potenciales frente a los gastos de realizar la campaña.
2. Juegos de colaboración
En contraste con lo anterior, también existen situaciones en las que varios agentes no compiten, sino que pueden beneficiarse cuando cooperan.
Imaginemos una cadena de suministro con tres eslabones: el fabricante, A, y dos vendedores, B y C (mayorista y minorista respectivamente). Estos tres jugadores tienen la opción de formar una alianza y tomar decisiones conjuntas para afrontar la incertidumbre del mercado. Con esa decisión, estiman que podrán aumentar sus beneficios en 475 u.m.
Si todos colaboran, deberán repartirse los beneficios. ¿Pero cuál sería la asignación justa? ¿Qué valor tiene cada una de estas empresas en la alianza? A priori, no parece una pregunta fácil de responder. ¿Cómo se podría calcular este valor? Matemáticamente, una solución a esta pregunta sería utilizar el valor de Shapley. Este valor considera lo que cada agente contribuye al colaborar con los demás, evaluando cuánto ganan o dejan de ganar el resto de participantes. Por ello, aquellos agentes más valiosos deberán obtener mejores resultados que los que aportan menos o pueden ser prescindibles.
- En este caso, el fabricante es imprescindible. Sin él no hay productos que B y C puedan vender, es decir, si A no participa en la alianza, no habrá beneficios para nadie.
- Por el contrario, A no necesita a B y a C. Puede vender sus productos a otras empresas y obtener un beneficio de 100 u.m.
- Si A y B trabajan juntos, podrían repartirse 300 u.m.
- Mientras que, si la alianza se forma con A y C, se repartirían 375 u.m.
Una forma sencilla de calcular el valor de Shapley sería calcular el beneficio que merece cada una de las empresas al formar las distintas posibles alianzas si se unieran por orden. Esto es, considerar el valor de cada empresa en solitario y de las alianzas que se van formando conforme se van uniendo los participantes uno a uno.
Por ejemplo, para la combinación CAB:
- C no obtiene nada porque, por su cuenta, no podría obtener beneficios.
- Si a la alianza con C se une A, el valor de estos dos juntos alcanzaría 375. A se llevaría 375-0=375 en su totalidad.
- Finalmente, al unirse B, éste gana la diferencia entre el valor total alcanzado por los tres y lo que ya se han llevado A y C anteriormente: 475 – 375 – 0 = 100
Si se realizan estos cálculos para todas las posibles alianzas entre estas tres empresas, el valor de Shapley de cada una se obtiene de la media de lo que ha obtenido en todas las permutaciones.
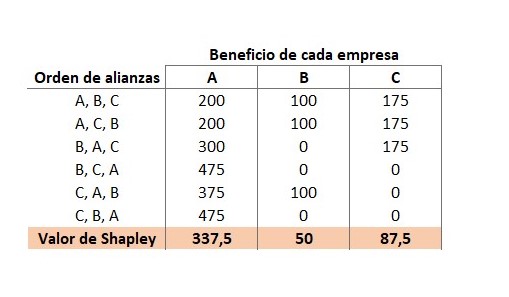
El valor de Shapley permite conocer cuál es el valor mínimo que cada uno de los agentes debería exigir si decide colaborar con los demás. La empresa A no sólo es quien más aporta, sino que, también es imprescindible para formar la alianza, por ello, su valor y porción de los beneficios es mucho mayor.
Cuando las tres empresas negocien las condiciones de esta alianza, A no deberá aceptar menos de 337,5 u.m. De esta manera, podrán beneficiarse los tres de la colaboración y podrán repartirse los beneficios justamente, de acuerdo a lo que cada uno es capaz de contribuir.
Para problemas como los descritos, la teoría de juegos permite ilustrar las interacciones de los agentes en el mercado y los posibles resultados de adoptar una estrategia u otra. Esta herramienta no sólo facilita la comprensión de muchos de estos problemas, sino que puede constituir la forma de representar otras situaciones o fenómenos, caracterizados por las decisiones e interacciones de los agentes, que no podrían explicarse de otra manera.
- Análisis de seguridad de la computación en la nube (cloud computing). La teoría de juegos permite reflejar la relación entre un usuario de este servicio y un posible atacante, determinar los riesgos y las posibles estrategias de cada uno e, incluso, definir en qué circunstancias las vulnerabilidades deben ser cubiertas por el usuario o por el proveedor del servicio.
- En los mercados de energía que operan con la tecnología blockchain, generadores y consumidores pueden comercializar al margen de los mercados tradicionales. La teoría de juegos permite modelar las interacciones de todos los agentes involucrados y representar el comportamiento del precio según sus acciones.



