
Game theory can provide a valuable point of view for decision-making.
Daily, each company faces complex decisions about its operations. For some of these decisions, the outcome of the decision is not conditioned by the decisions of others, but in many cases, it is. The result not only depends on the action or strategy adopted but is also affected by the decisions of others.
It may be easy to decide to improve predictions of customer demand or to automate the production process if the return on investment is positive. However, when decision-making encompasses those of a strategic nature and involves more agents, not only can it be complex to quantify the results of such actions, but also to interpret them.
In this context, a branch of mathematics known as game theory emerged, which is closely related to behavioural economics. Game theory makes it possible to represent common situations of competition or cooperation of some agents, through simplifications (games). This allows determining the best strategy for each situation, given the expected behaviour of the players. Below, we will see two examples to illustrate how to apply game theory to common situations of competition or collaboration.
1. Competition games
To increase its market share, company A can consider different strategies, such as lowering the prices of its products or investing in an advertising campaign. The first thing A will do is to economically analyze these options, so it will have estimates of the return on investment of both, but is this information enough?
If company A has competition, it would like to consider what the competition is going to do. What will company B, which sells similar products do? Is B likely to copy A’s strategy?
- If both companies decide to invest in large advertising campaigns, they will incur high costs, but will not change their income, since the total number of customers in the market remains the same.
- If B does not carry out such a campaign, A would greatly benefit from it and would attract B’s customers. And the same would happen in the reciprocal case.
- Ultimately, if neither of them invested, nothing would change between them.
Since A analyzed the alternatives to invest and not to invest, we can represent these decisions in a matrix. Each cell (a, b) contains two values corresponding, respectively, to the benefits of A and B when A chooses the strategy in the row (in orange) and B the strategy in the column (in black). That is if A does not invest, but B does: A would lose CU10. (currency units) and B would earn CU5.
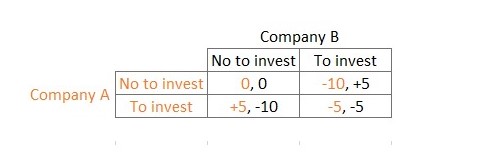
If the two companies choose the same strategy, their market share and income will not increase. Although if both have decided to carry out the campaign, both will have to bear those costs. Whereas, if they differ, the one that has invested will attract the other’s clients and will more than exceed the advertising costs.
With such a simple matrix, the effects of a non-trivial interaction and the possible results are modelled according to the decisions made by each company. The best decision for the two companies, in isolation, would be to invest. However, the best joint decision would be not to, even if this implies a clear opportunity cost for both companies and the temptation to change strategy at any time to win over the other.
Can A trust that B is acting rationally and deciding not to invest? What if it’s a repeated decision they make every year, like a Christmas campaign? Will A’s decision be influenced by what B decided to do the previous year? What if the payoff matrix is not symmetrical and one company has more to lose than another? Or how would the situation change if there were more than two companies?
This game represents a simplification by not taking into account the previous questions and many other factors, however, it provides a more complete perspective into this problem and provides valuable information that would not have been taken into account had A only considered potential income versus the expenses of carrying out the campaign.
2. Cooperation games
In contrast to the above, there are also situations in which several agents do not compete, but can benefit when they cooperate.
Let’s imagine a supply chain with three links: the manufacturer, A, and two sellers, B and C (wholesaler and retailer respectively). These three players have the option of forming an alliance and making joint decisions to deal with market uncertainty. With that decision, they estimate that they will be able to increase their profits by CU475.
If all of them collaborate, the benefits must be shared. But what would be the fair allocation? What is the value of each of these companies in the alliance? A priori, it does not seem like an easy question to answer. How could this value be calculated?
Mathematically, a solution to this question would be to use the Shapley value. This value considers what each agent contributes by collaborating with the others, evaluating how much the other participants earn or lose by the agent’s presence in the alliance. For this reason, those more valuable agents should obtain better results than those that contribute less or can be dispensable.
- In this case, the manufacturer is imperative. Without it, there are no products that B and C can sell, that is, if A does not participate in the alliance, there will be no benefits for anyone.
- In contrast, A does not need B and C. It can sell its products to other companies and make a CU100 profit.
- If A and B work together, they could share CU300 in profit.
- Whereas, if the alliance is formed with A and C, then CU375 would be shared.
An easy way to get the Shapley value would be to calculate the profit each of the companies deserves from forming the different possible alliances if they joined in order. That is, consider the value of each company and the coalitions that are formed as the participants join one by one.
For example, for the CAB combination:
- C makes nothing because, on his own, he could not make a profit.
- If A joins the alliance with C, the value of these two together would reach 375. A would take 375-0 = 375.
- Eventually, when B joins, it earns the difference between the total value reached by the three and what A and C have already taken previously: 475 – 375 – 0 = 100
If these calculations are made for all possible alliances between these three companies, the Shapley value of each one is obtained from the average of what it has benefited in all permutations.
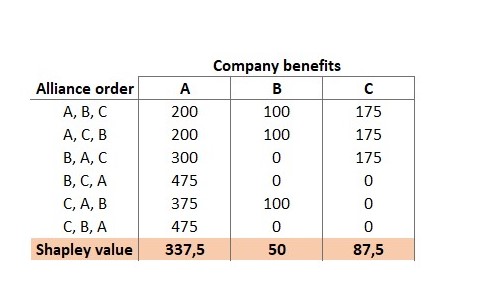
The Shapley value can be interpreted as the minimum amount that each of the agents should demand if they decide to collaborate with the others. Company A is not only the one who contributes the most, but it is also essential to the alliance, therefore, its value and portion of the benefits should be much larger.
When the three companies negotiate the terms of this alliance, A must not accept less than CU337.5. Thus, the three will be able to benefit from the collaboration and the benefits will be distributed fairly, according to what each company is capable of contributing.
For problems such as those described above, game theory makes it possible to illustrate the interactions of agents in the market and the possible results of adopting one strategy or another. This tool not only facilitates the understanding of many of these problems but can also be the way to represent other situations or phenomena characterized by the decisions and interactions of the agents, which could not be explained in any other way, for example:
- Cloud computing risk assessment. The interactions between an attacker and the user of a cloud computing service can be modelled using game theory. Understanding this relationship, the risk in the system can be evaluated and determined whether it should be fixed by the cloud provider or the tenant of the system.
- Electricity trading in energy blockchain environments allows buyers and sellers to operate out of traditional energy markets. With game theory, the interactions among agents can be modelled and price behaviour can be understood through the agents’ actions.


