This is an abbreviated excerpt from the introduction to Franco Peschiera’s PhD thesis entitled: “Exact and Heuristic Methods to Optimize the Flight and Maintenance planning of Military Aircraft”.
The maintenance industry
Be it a house, a car or a nuclear power plant, maintenance is a key consideration when building or acquiring a new asset. For example, the yearly maintenance costs for a house can equal 1-4% of the purchase price. This cost represents the price to pay to keep the acquired asset in normal operation conditions and prolong its life as long as it is economically possible.
Maintenance is quite expensive. Usually, it involves several specialized labour-intensive tasks that are hard to automate. On top of that, in a quest for lower production costs, companies have made products harder and harder to repair or maintain. Canada estimates its companies spent 3.3% of GDP on repairs in 2016, more than twice as much as the country spends on research and development. Although the value of a good maintenance policy is usually hidden behind the uneventful and correct functioning of a system, the cost of a lack of maintenance of public infrastructures can be measured from time to time. This became all too evident recently with the collapse of the Genoa bridge in Italy. The lack of investment in maintenance was one of the main reasons for this tragedy that caused the death of 43 people in August 2018.
In the aircraft industry, maintenance is done via various types of maintenance operations also known as checks. These checks vary in frequency, duration and thoroughness. The frequency is usually measured in a combination of flight hours, takeoff-landing cycles, and calendar months; the duration, in months or man-hours of labour.
Planning maintenances
The Flight and Maintenance Planning (FMP) problem, first presented by Barnhart in one of her two 1998 papers, studies how these maintenance operations are scheduled and how flight activities are assigned to a fleet of aircraft along a planning horizon.
In the civilian variant of the FMP, by far the one that has received the most attention, aircraft need to be routed along different destinations by assigning them flight legs in order to build daily trips. Checks are done during the night and are usually limited to A and B type checks. The planning horizon covers several days (e.g. this method proposed by Sriram uses 7 days). The objective is usually to reduce the overall cost or to maximize total profit for the plan.
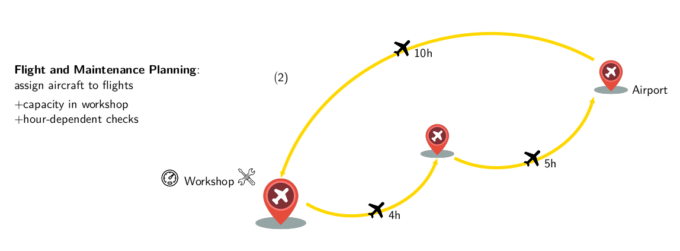
In the military variant, which we call the Military Flight and Maintenance Planning (MFMP) problem, flights (which are called missions) always return to the airbase and so no routing is performed. Checks consist of B, C and D types. The planning horizon covers a few months or several years. The objective is usually to maximize the operational status of the fleet while minimizing the total number of checks.
In most air forces, a derivative of the Sliding Scale Scheduling Method (SSSM) is used to plan the mission assignments for a fleet of aircraft. This method consists of a simple heuristic that attempts to distribute remaining flight hours among aircraft in a ladder-like distribution, i.e., there is a constant probability of finding an aircraft for each possible amount of remaining flight hours. When an aircraft passes a certain threshold of flight hours, it is sent for a check. In the example below, Aircraft “944” has the most surplus remaining flight hours (bank time) with respect to the curve and thus should fly the next mission.
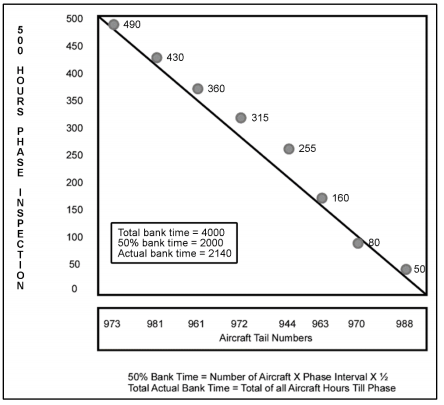
This technique attempts to distribute the flight load uniformly between each aircraft and is well suited when the future mission requirements are known and do not change over time, the fleet is homogeneous and the initial status is more or less well distributed. As can be expected, these hypotheses rarely apply in real life and so more sophisticated techniques are needed if good quality maintenance plans are to be obtained for realistic situations.
Recently, improving the quality of these maintenance plans has become a priority for many governments. In particular, the French Air Force became interested in mathematical solutions to schedule maintenance for the Mirage 2000 fleet after it was revealed that increases in maintenance costs had not been followed by improved availability of aircraft.
There are two main questions that need to be answered when improving maintenance decisions: when is the maintenance needed (prediction) and when is the maintenance actually done (prescription).
Calculating maintenance needs has usually consisted of what is called preventive maintenance. In preventive maintenance, a simple rule is established that ties usage and maintenance need, e.g., an aircraft cannot fly more than 500 hours without maintenance. In contrast, predictive maintenance involves the analysis of historical data to estimate windows of time when maintenance has to be done so as to guarantee a risk of failure under a certain threshold. According to the US Air-Force tests on command-and-control planes, the use of predictive maintenance could reduce unscheduled work by a third.
Regardless of how we calculate those maintenance needs, a suitable maintenance schedule is essential in order to produce an efficient overall plan. To achieve this, those time windows are taken together with resource capacities and future usage planning, among other information, in order to produce an actual maintenance schedule that is feasible and satisfies the needs of its planners.

The value of a good maintenance plan
The difference between any maintenance plan and a good one is important. As the resources needed to actually perform the checks are expensive and the expertise required is highly specialized, the capacity to provide this service is usually quite limited and inflexible. As a result, a plan that does not allocate the capacity optimally may end with more grounded aircraft waiting for a check in some periods while in other periods the capacity usage is not at maximum. This unavailability reduces the actual potential of the fleet and thus requires having even more aircraft to satisfy a certain fleet potential.
The actual cost of a maintenance plan is measured by the number of checks needed to comply with all the mission requirements: the lower that number is, the better. Although costs for these checks are not public in the case of military aircraft, the actual costs for type D checks in Boeing aircraft range between 1 million dollars and 6 million dollars depending on the aircraft model. In France, the total yearly cost of military aircraft maintenance rose from 3.2 billion euro in 2012 to 4 billion euro in 2017. A good maintenance plan will try to use each aircraft as much as possible before scheduling a check in order to minimize the number of remaining flight hours that are “lost” when the check is done and flight hours are reset to their maximum.
“A good maintenance plan will try to use each aircraft as much as possible before scheduling a check in order to minimize the number of remaining flight hours that are “lost” when the check is done and flight hours are reset to their maximum.”
Maintenance planning in practice
Finally, the planning of maintenance is usually done manually (in an Excel spreadsheet), which is extremely time consuming. This limits the number of scenarios that can be evaluated before taking a decision and increases the reaction time when dealing with new information that requires to change the original plan. As a result, robustness and flexibility are lost as part of the planning process.
Thus, the need for efficient and reliable flight and maintenance planning is clearly a priority both in commercial as in military contexts. Nevertheless, producing such a detailed plan for a sizable fleet while planning for a long-term horizon and taking into account the multiple objectives inherent to long-term planning is not an easy task.
Operations Research techniques are specialized in solving combinatorial problems such as the MFMP in order to produce very good quality solutions (often optimal) given a set of constraints and an objective function. The success in applying these techniques to a new, difficult, problem requires a combination of domain expertise and profound theoretic background. The latter consists of a deep study on the structure of the underlying mathematical problem and the research of innovative solution approaches that are compatible with that problem. We will detail such analysis in future posts in this blog.