Blog

Inspired by kaggle competitions and other similar events, a few months ago we decided to arrange an internal optimization hackathon at baobab.

For those who are not familiar with the term, a hackathon (a combination of “hack” and “marathon”) is a meeting in which several groups compete almost without interruptions to solve a predefined problem. It is an event focused on a specific challenge that motivates both creative thinking and teamwork. It usually leads to very innovative solutions.

In our hackathon we decided to compete on how to solve a combinatorial problem in the most efficient way. Eight people stepped up and joined in. The event officially took two Friday afternoons, although we extended the deadline to allow the teams enough time to polish their proposal and make a unified benchmark. We also decided (after a bit of negotiation) to use python as our development language in order to make the comparison among solutions easier.

The challenge

We decided to dedicate the hackathon to solving a variant of a classic job scheduling problem. We started with a set of non-interruptible jobs that had to be carried out. Some jobs take precedence over others. For example, if job A takes precedence over job B, job A must finish before job B begins.

There are also two types of resources. Renewable resources are consumed in each period in which the job is performed and their capacity is recovered at the beginning of a new period. Non-renewable resources are consumed only once per job and are never recovered.

Finally, each job can be performed in different “modes”. Depending on the mode, the duration of the job and its resource consumption will vary.

The objective is to find the schedule that, by choosing the mode and starting period for each job, uses the fewest possible periods (shortest makespan), without spending more resources than are available.

The following table presents the input data for the first 5 out of 18 jobs in an instance. Each job and each mode has a predefined duration and consumption of four resources: “R 1” and “R 2” (renewable), “N 1” and “N 2” (non-renewable). The capacities of each resource are shown between brackets. The “Dependencies” column shows the other tasks that have to finish before starting the current one (for example: task 1 takes precedence over task 2, 3 and 4).

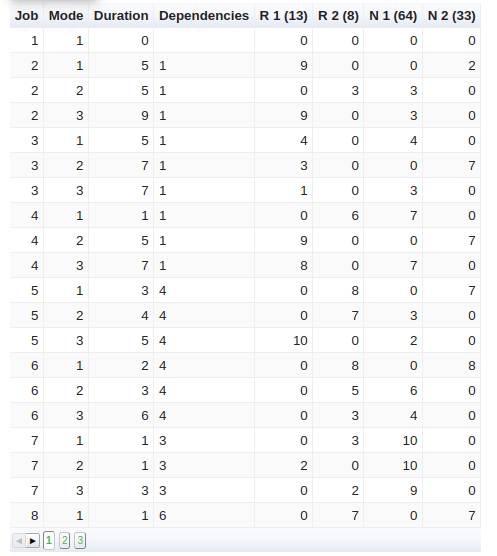
For this competition we used approximately sixty different instances similar to this one.

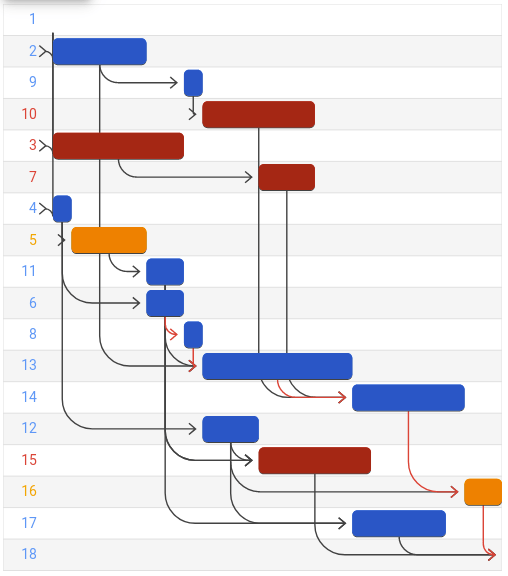
The following figure shows the optimal solution to this instance on a Gantt chart. Each row represents a job and its colour indicates the mode it was performed (blue: 1, orange: 2, red: 3). The black arrows represent the dependency relationships between the jobs.

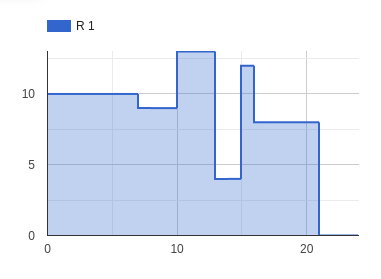
The following graphs show that the maximum use of resources “R 1” and “R 2” reached 13 and 8, respectively, which fall within the acceptable range, so not using more renewable resources than those available.

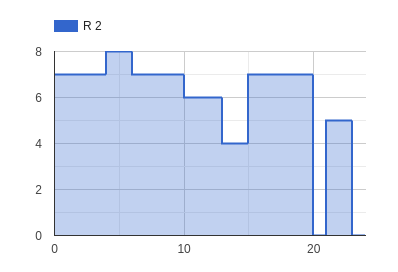Methodology

Methodology was as follows:

• We created a public repository (which you can look at): https://github.com/baobabsoluciones/hackathonbaobab2020
• As a starting point, we gave a python base code for reading the input data, generating output files with the solution and checking of a solution.
• We created an example algorithm that generated a quick and dirty solution which we called “default”.
• We designed some unit tests to validate that a solution method worked correctly.
• Each team delivered its solution through a Pull Request.
• We used a set of sixty random instances to test the results.

Techniques

Three groups developed and delivered a resolution method. At baobab we have a much stronger training in linear programming models and therefore two groups chose techniques based on MIP (Mixed Integer Programming). Despite certain lack of experience, one group ventured to try a different paradigm: Constraint Programming (CP).

Although it was not a condition, all models were implemented exclusively using open source solvers.

The table below summarizes each of the techniques, which we will compare later. You can find more detail in our github repository.

Name	Technique	Description
default	Example heuristic	Jobs are chosen one by one, respecting dependencies and never doing more than one job in parallel.
ortools	CP	Pure Constraint Programming model. Solver: CP-SAT.
Iterator_HL	MIP + heuristic	Heuristic decomposition in MIP models. Solver: CBC.
loop_EJ	MIP + heuristic	Heuristic decomposition in MIP models. Solver: CBC.

Results

The efficiency of a resolution method can be measured in many ways. The most immediate one is based on the quality of the solution after a set time limit. If we decide to follow this path, the quality of the solution can be measured in two ways: to what extent the requirements were met (precedence, use of resources, etc.) and degree of compliance with the target (that is: the number of periods required by the schedule to perform all jobs, or makespan). In addition, for exact methods such as those used in this competition, the time to prove that a solution is optimal is also measured.

Let’s start with requirements: the following graph shows the number of “errors” in the solutions delivered by each method. Every “error” is a breach of a requirement. The graph shows two techniques that return feasible solutions: “ortools” and “Iterator_HL”. “Default” and “loop_EJ” returned non-feasible solutions for a large number of instances, and were therefore practically ruled out.

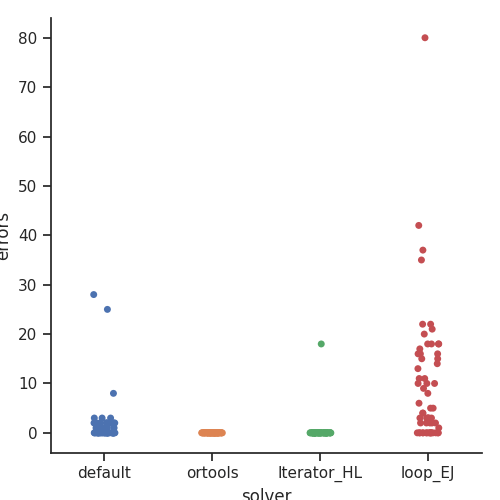
Regarding the second quality measure: total makespan, the following graph shows a relative comparison of the quality of each instance. To that end, we used the “ortools” technique as a reference, as it was the one that returned solutions with the fewest errors (none). The “loop_EJ” technique and the “default” technique returned shorter schedules in some instances, but the results were not valid due to the amount of errors they contained.

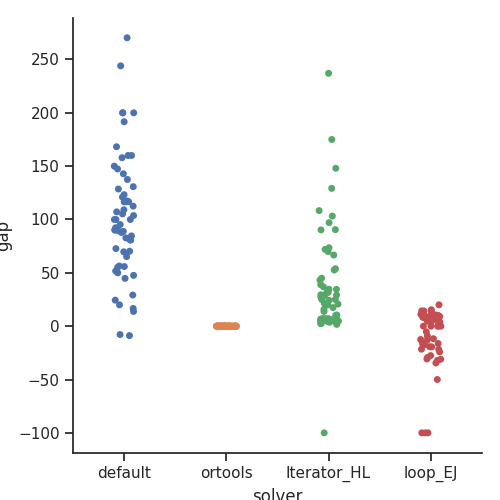
Finally, the following table shows mean resolution times for each technique and each scenario (each scenario contains five instances). The two MIP-based techniques (“Iterator_HL” and ”loop_EJ”) presented much longer durations. In particular for the largest instances (j30.mm). “Ortools” had no trouble.

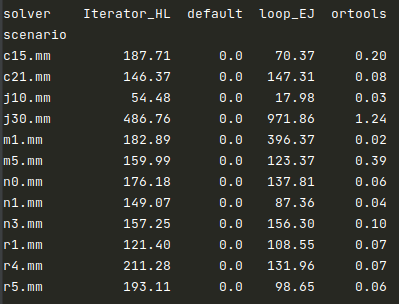
“ortools” was the clear winner of this hackathon. By any metric (time, quality of solution) it turned out to be the best by orders of magnitude, most of the time.

Conclusion

Real projects come with deadlines and tight schedules and we cannot afford the time to rigorously test and compare new techniques against those we already know. That’s why hackathons like this one are very useful for exploration and innovation. In particular, we had never worked with the “ortools” library or the CP-SAT solver before and it was a very pleasant surprise to see that, for “pure” scheduling problems, this open source solver works very well.

However, there are still many other interesting techniques to try with this problem. For example, dynamic programming and metaheuristics. Do you dare to suggest and implement a new technique? You just need to clone the public repository, follow the instructions to add a new method and make a Pull Request for us to add it to the benchmark.

The gauntlet is down.