Mejorar la asignación de ambulancias a bases en una ciudad, cubriendo toda el área y atendiendo a todos los residentes de la mejor manera posible, implica un tiempo de atención menor a una emergencia con el mismo número de recursos. Las situaciones en las que puede ser necesaria una ambulancia son potencialmente críticas. El dimensionamiento matemático de un servicio de ambulancias es un problema para el que vale la pena encontrar la mejor solución posible.
El problema no es sencillo de resolver. Emplear métricas basadas en medias o datos antiguos es engañoso, especialmente si no hay suficientes registros. Los enfoques basados en modelos tipo k-means o de cobertura son pobres. En media una ambulancia puede tener buenos tiempos de intervención, pero si todas las ambulancias de una base están ocupadas, los tiempos empeoran más de lo aceptable.
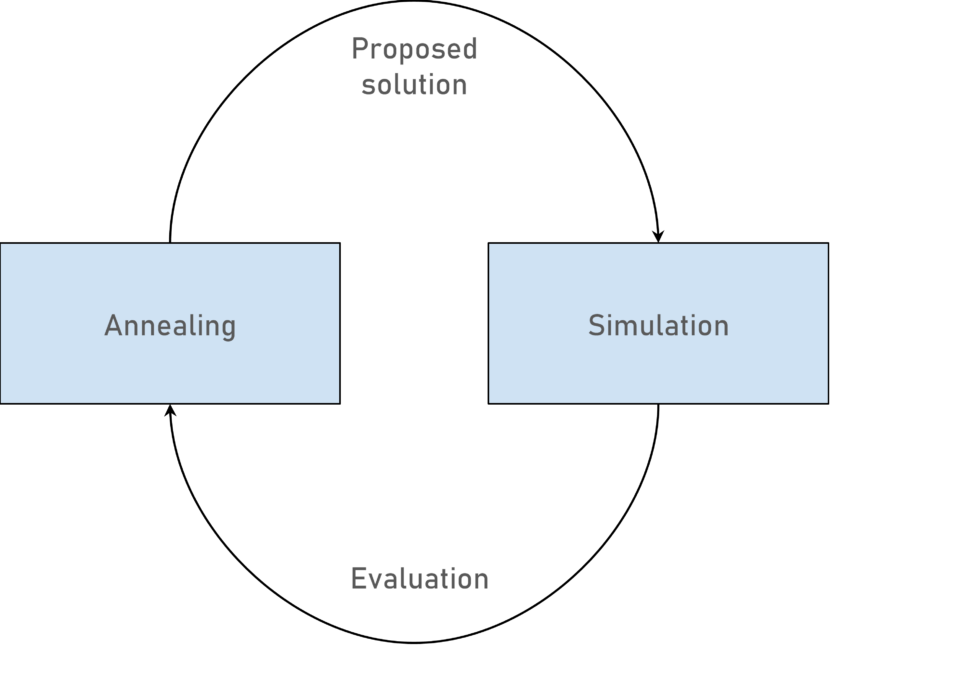
Por ello, en baobab hemos planteado una metodología diferente basada en Recocido Simulado (Simulated Annealing) y simulaciones que hemos desarrollado internamente como parte de nuestra generación de conocimiento.
A grandes rasgos el método consiste en lo siguiente:
- Crear una solución empleando un algoritmo sencillo y, con ello, establecer cuántas ambulancias hay inicialmente en cada base
- Evaluar la solución no mediante una expresión analítica sino mediante un modelo de simulación para caracterizar cuál sería el funcionamiento esperado en la realidad. El modelo nos devolverá un indicador de idoneidad de la solución, que llamaremos energía y que deberá ser lo más bajo posible.
- Recoger la información de la simulación. Según el resultado, la solución evaluada se descarta o se admite como nueva solución actual. La solución actual se empleará para crear una nueva solución.
- Repetir los pasos 2 y 3 y conservar la mejor solución
Simulated Annealing (Recocido Simulado)
El recocido simulado es un algoritmo de búsqueda metaheurística para problemas de optimización. Esto quiere decir que en lugar de calcular sistemáticamente la solución óptima a un problema, generalmente por no disponer de suficiente capacidad de cálculo, muestrea el espacio de soluciones empleando ciertos supuestos hasta encontrar una solución suficientemente buena.
El nombre de recocido simulado viene inspirado por la técnica metalúrgica del recocido, que consiste en el calentamiento y enfriamiento controlados de un material para aumentar las dimensiones de sus cristales y eliminar sus defectos.
En este caso aplicamos el siguiente esquema.
- A partir de una solución inicial obtenida de manera sencilla, incluso aleatoria (asignación aleatoria de ambulancias a bases), calculamos mediante simulación la energía de la solución. Con gran probabilidad, esta energía será alta.
- Hacemos un cambio en la solución inicial (reasignamos alguna ambulancia a otra base), calculamos la energía de esta nueva solución y comparamos esta con la anterior.
- Si la diferencia de energía es negativa, es decir, la nueva solución es mejor que la previa, desechamos la solución previa, mantenemos la nueva y repetimos el paso anterior.
- Si la diferencia de energía es positiva, es decir, la nueva solución es peor que la previa, a fin de huir de óptimos locales aún podemos conservar la nueva solución si la diferencia de energía es pequeña. Para ello calculamos un factor p entre 0 y 1 que es más pequeño cuanto mayor sea la diferencia de energía y menor sea otro parámetro que llamaremos temperatura, y a continuación generamos un número aleatorio entre 0 y 1. Si este número es menor que p, aceptaremos la nueva solución.
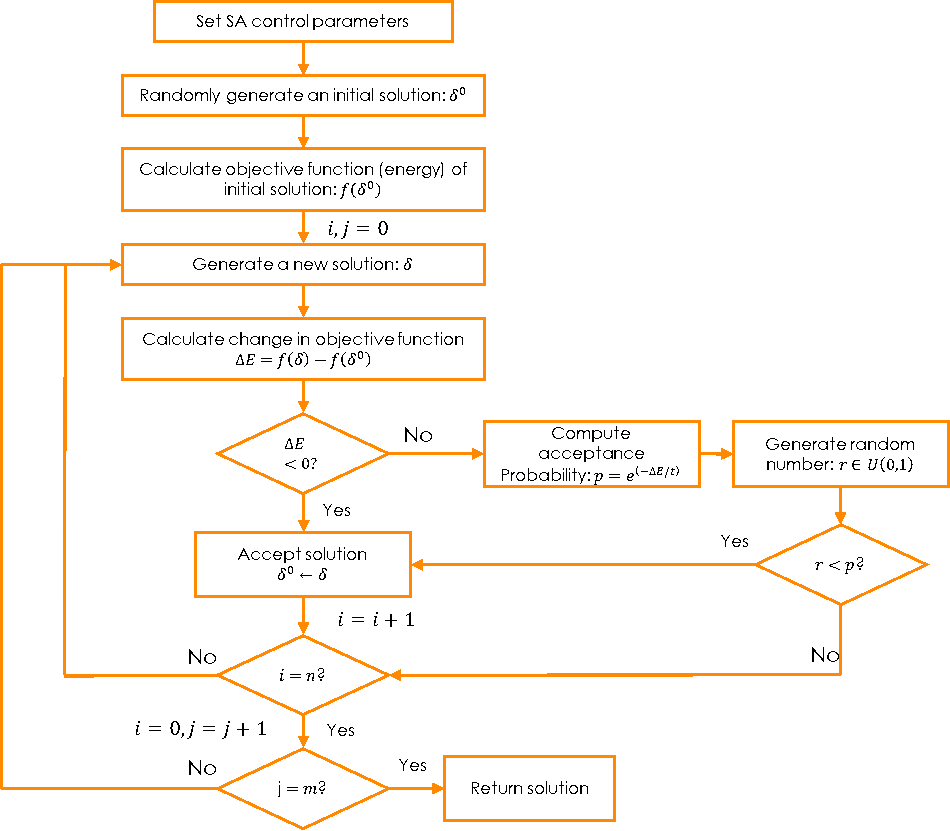
Este proceso está insertado en dos bucles que condicionan durante cuánto tiempo se ejecuta. Un bucle interno cuenta cuántas soluciones se calculan para cada temperatura. Un bucle externo cuenta cuántos valores de temperatura se considerarán, de mayor a menor. Es decir, iremos reduciendo la temperatura del algoritmo un número predefinido de ocasiones.
La simulación
El objetivo de la simulación es medir la idoneidad de cada plan de asignación de ambulancias a bases (las soluciones). Para ello genera emergencias ficticias en diferentes localizaciones del área analizada, calcula la distancia desde cada uno de los vehículos disponibles y asigna el vehículo más cercano; si fuese necesario, considera el tiempo y la distancia que el vehículo dedicaría a dirigirse al hospital y regresar a su base. La simulación considera que el vehículo ya está disponible para atender otra emergencia en el trayecto de regreso a la base.
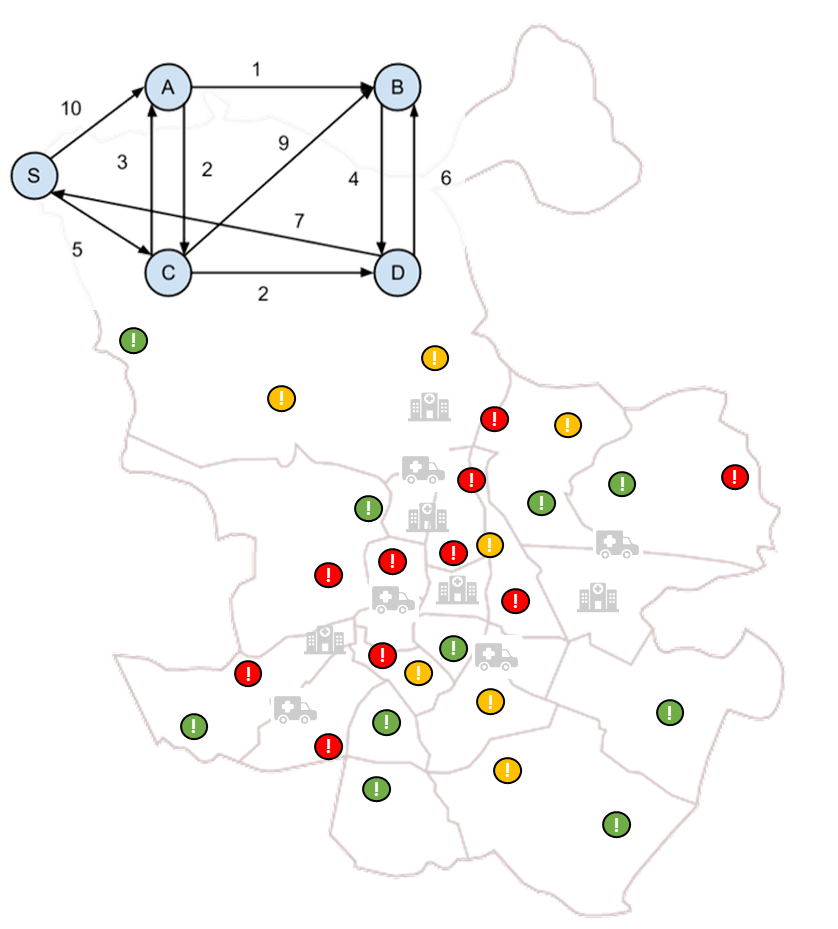
Para facilitar el desarrollo y reducir los tiempos de cómputo, en la simulación se divide la ciudad en zonas y se define un nodo para cada zona, al que se asignarán las emergencias generadas en la zona correspondiente. De esta manera, la ciudad se representa como un mosaico de zonas y una red de nodos conectados entre sí. De esta forma, los tiempos de desplazamiento entre cada nodo y sus nodos adyacentes se pueden determinar mediante APIs públicas y es posible aplicar el algoritmo de Dijkstra para calcular la ruta más corta entre dos nodos cualesquiera.
Resultados
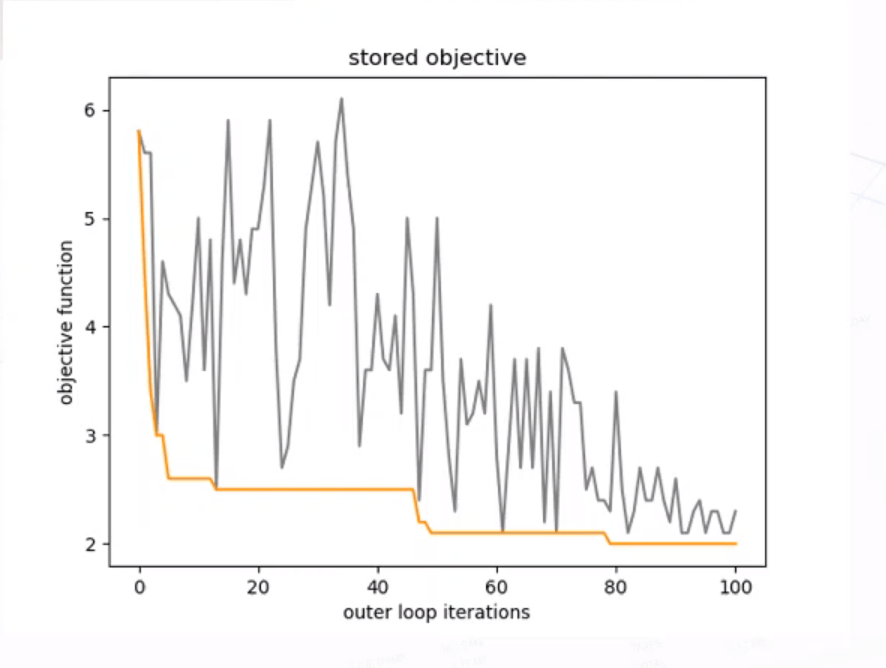
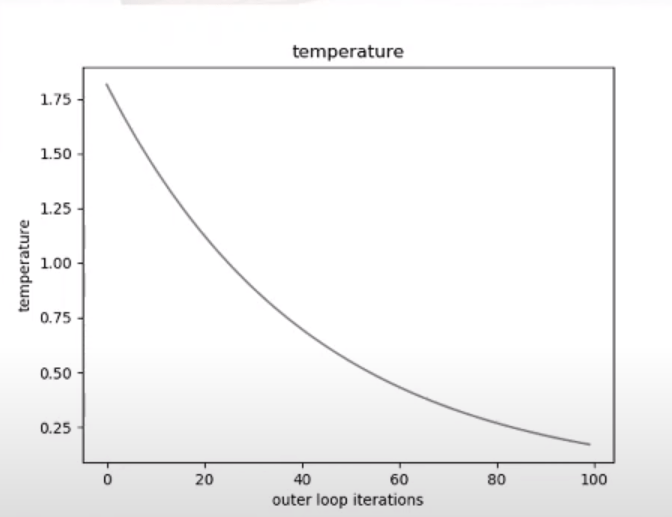
Este método permite abordar un problema de difícil resolución por métodos más tradicionales. Las gráficas inferiores muestran cómo cambia la temperatura y cómo evoluciona la probabilidad de aceptar una nueva solución en una ejecución del problema con 100 valores de temperatura (bucle externo) y 20 iteraciones por cada valor (bucle interno).
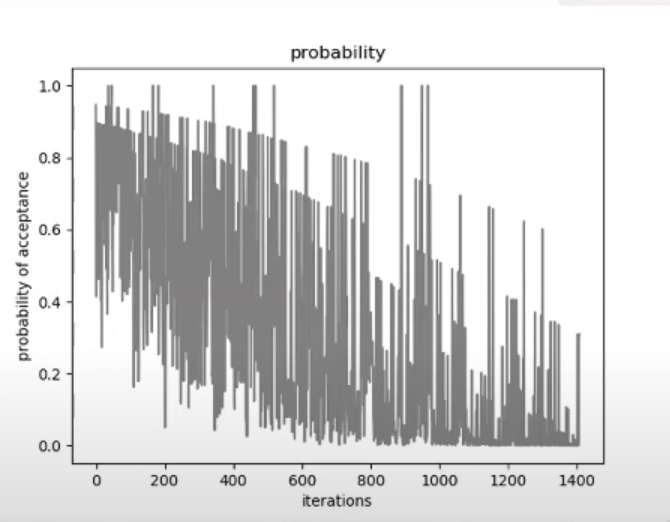
La gráfica inferior muestra claramente cómo decrece la energía de la mejor solución encontrada para cada temperatura y cómo durante el proceso se admite explorar soluciones que son peores para, precisamente, poder acceder a otras que ofrezcan un mejor resultado (a veces para llegar a la cima más alta hay que descender por un valle para volver a ascender después)